
Le théorème de Jordan est célèbre pour être particulièrement simple à comprendre, mais particulièrement ardu à démontrer rigoureusement. Prenez une feuille de papier et un crayon, puis tracez une ligne continue (c’est-à-dire sans lever le crayon) qui part d’un point et revient à ce même point sans jamais se croiser elle-même. En bref, une ligne qui fait une boucle. Le théorème affirme alors que la ligne divise la surface du papier en deux zones : la zone intérieure et la zone extérieure. Bien que ce résultat semble relever du simple bon sens, il ne fut complètement démontré qu’en 1887 par le mathématicien Camille Jordan.
Ce résultat est aussi parfois nommé « théorème du berger », car pour garder leurs moutons, les bergers ont tout intérêt à faire usage de clôtures jordaniennes.
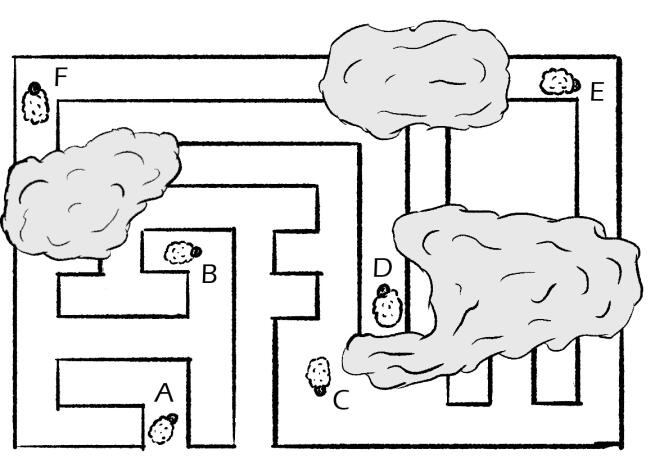
L’image ci-dessous montre une telle clôture vue du ciel. Nous pouvons être sûrs que le berger a bien fait son travail : la clôture forme une boucle et délimite donc une unique zone intérieure dont il est impossible de sortir sans sauter par-dessus. Malheureusement, des nuages cachent certaines zones et le berger ne se souvient plus très bien de la forme de son enclos.
Pour chacun des moutons A à F, est-il possible d’indiquer au berger s’il se trouve à l’intérieur ou à l’extérieur de l’enclos, malgré la présence des nuages ?
Retrouvez les énigmes précédentes en cliquant ici
Contribuer



















L’espace des contributions est réservé aux abonnés.
Abonnez-vous pour accéder à cet espace d’échange et contribuer à la discussion.