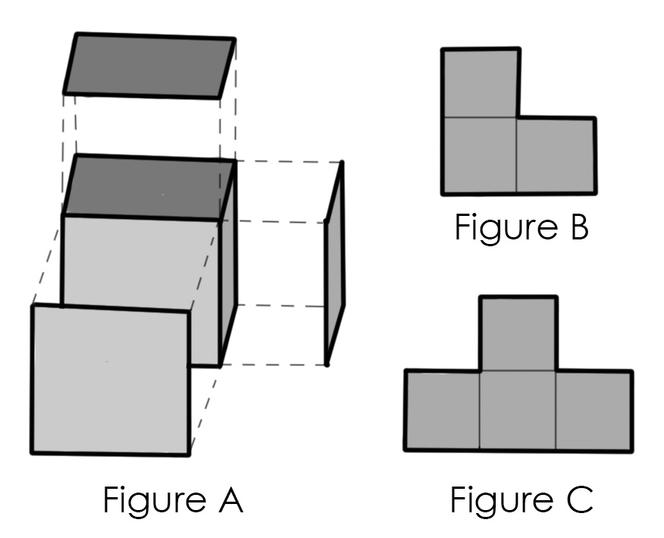
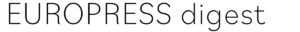Il existe certaines formes géométriques en 3D qui ont la même silhouette selon qu’on les regarde de face, de côté ou de haut. C’est le cas du cube : si vous l’observez selon chacune des trois directions parallèles à ses côtés, vous verrez toujours un carré, comme illustré par la figure A.
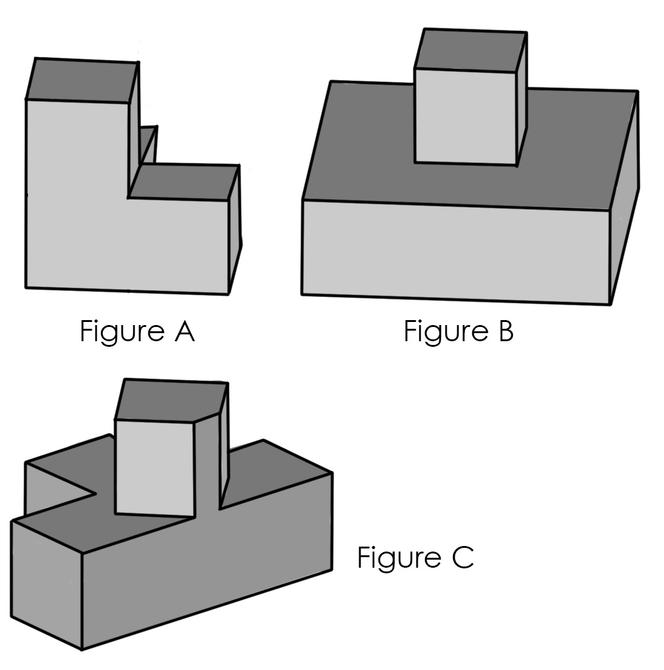
Est-il possible de trouver une forme en 3D dont les trois silhouettes (de face, de droite et de haut) ont la forme d’un trimino en L, semblable à celui présenté par la figure B ? Et qu’en est-il d’une forme dont les trois silhouettes auraient une forme de tétramino en T, comme celui de la figure C ?
Pour voir le détail, cliquez sur une ligne
Tout refermer
.elliat emêm al tnemeriassecén sap siam, emrof emêm al riova tneviod setteuohlis seL
Pour trouver la forme à silhouette en L, il suffit de partir du cube et de découper la forme de L dans chacune des trois directions. On trouve alors la forme illustrée par la figure A. Pour la forme à silhouette en T, il y a une subtilité. On peut trouver une forme ayant une silhouette en T vue de face et vue de droite en découpant dans le cube, comme précédemment : on trouve la figure B. Mais, vue de haut, la figure B a encore la forme d’un carré et il n’est pas possible de découper le T parallèlement aux côtés du cube sans rogner sur les figures vues de face ou de droite. Il est donc nécessaire de placer le T du haut en diagonale, de façon qu’il occupe toute la largeur et toute la longueur du carré. On obtient la figure C. Notez que, de cette façon, la silhouette du haut est légèrement plus grande (d’environ 6 %) que celles de face et de droite.
